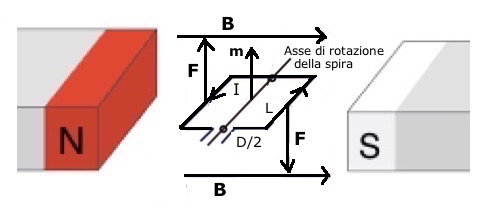
SPIRA RETTANGOLARE IN UN CAMPO MAGNETICO UNIFORME

L'analisi del comportamento di una spira rettangolare percorsa da una corrente continua I ed immersa in un campo magnetico uniforme B rappresenta il punto di partenza per la comprensione del funzionamento di un motore elettrico in corrente continua a magneti permanenti.

Facendo riferimento alla Fig.1, dove il piano della spira e' stato assunto inizialmente parallelo alle linee di forza del campo magnetico B, si nota che su ciascun lato della spira, perpendicolare alle linee di forza di B, agisce una forza F:

Fig.1

La direzione ed il verso della forza magnetica F, subita dalla corrente I, sono dati dalla regola della mano destra, come mostra la seguente figura:

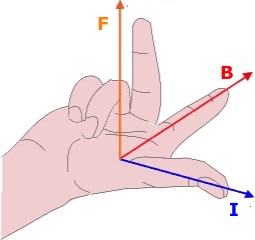Pollice, indice e medio della mano destra sono messi ad angolo retto uno rispetto all'altro; il pollice e' messo nella direzione-verso della corrente I, l'indice e' messo nella direzione-verso del campo magnetico B, il medio fornisce la direzione-verso della forza magnetica subita dalla corrente.

L'intensita' della forza F e' deducibile dalla Forza di Lorentz ed e' data dalla relazione:

F = I*L*B

In pratica, l'espressione della Forza di Lorentz riguarda una carica elettrica puntiforme q, in moto con velocita' v in un campo magnetico di intensita' B:

F = q v ^ B = q*v*B*senα

Tale forza, il cui nome e' dovuto al fisico olandese Hendrik Lorentz (1853-1928), e' nulla quando α = 0, cioe' quando la velocita' e' parallela al campo magnetico ed e' massima quando la velocita' e' perpendicolare al campo magnetico.

Se, al posto della carica q, si considera un tratto di filo conduttore infinitesimo dL, percorso da corrente I, la forza che agisce su di esso sara':

dF = I dL ^ B

Ipotizzando che il conduttore sia rettilineo e che tutte le grandezze siano uniformi, effettuando una operazione di integrazione si ottiene l'espressione della forza magnetica subita dalla corrente I:

F = I L ^ B (Forza di Laplace)

dove L e' la lunghezza del filo conduttore.

Dall'espressione vettoriale della forza magnetica F si comprende il motivo per cui i lati della spira, paralleli alle linee di forza di B, non sono soggetti ad alcuna forza (i vettori L e B sono paralleli), mentre la forza F agisce solo sui lati della spira perpendicolari alle linee di forza del campo magnetico B.

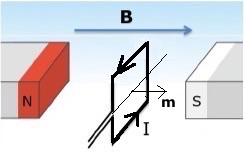
La coppia di forze, uguali e contrarie, che agisce sulla spira, ne determina una rotazione in senso orario. In pratica, se la spira fosse libera di muoversi essa cercherebbe di orientarsi nella direzione del campo magnetico B, fino al raggiungimento della posizione verticale, come illustrato in F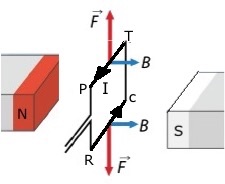ig.2:

Fig.2

Quando la spira e' in posizione verticale la coppia di forze non determina alcuna rotazione della spira.

E' possibile calcolare l'azione meccanica sulla spira che ne determina la rotazione; questa azione meccanica e' detta momento della forza. Si tratta di un vettore il cui modulo e' dato dal prodotto dell'intensita' della forza F per il braccio. Nel caso in questione il momento meccanico M che agisce sulla spira, provocandone la rotazione, e':

M = F*(D/2) + F*(D/2) = F*D

dove D/2 e' il braccio, ossia la distanza tra la forza F e l'asse di rotazione della spira.

Considerando che F = I*L*B, si ha:

M = I*L*B*D

poiche' L*D = S (superficie piana della spira), si puo' scrivere:

M = I*S*B

Il prodotto I*S = m e' il modulo del vettore momento magnetico m associato alla spira.

Il momento meccanico sara' pertanto:

M = m*B

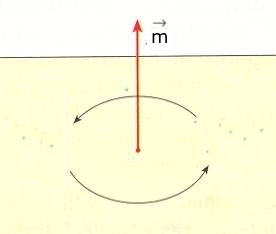
La direzione del vettore m e' ortogonale alla spira (Fig.1) ed il suo verso e' dato dalla regola della mano destra; ossia, bisogna orientare le dita secondo il verso della corrente, il pollice fornira' il veso di m, come indicato in F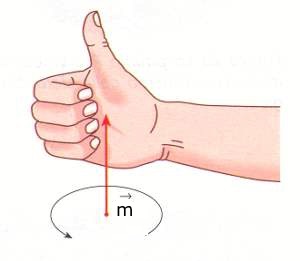ig.3:

Fig.3

Il momento magnetico m segue la spira nel suo movimento, come mostrato in Fig.2, dove m risulta essere parallelo alle linee di forza del campo magnetico B.

Ritorniamo ora ad esaminare proprio il caso in cui la spira abbia completato la sua rotazione e si sia disposta in posizione verticale come in Fig.2. Cio' che accade successivamente e' che, per effetto dell'inerzia, la spira superera' la posizione di equilibrio e non appena cio' accadra' nascera' un momento torcente che si opporra' al moto della spira e tendera' a riportarla nella sua posizione di equilibrio. La spira comincera' cosi' ad oscillare attorno a questa posizione, finche' l'attrito la fara' fermare. Per far sì che la spira continui a ruotare, bisognera' invertire, ogni mezzo giro il verso della corrente. In questo modo, con la corrente che circola in senso opposto, le forze cambieranno il loro verso e la coppia continuera' a favorire la rotazione della spira. In un motore elettrico cio' che provvede ad invertire il verso della corrente, ogni mezzo giro, sono i contatti striscianti tra il commutatore rotante e le spazzole fisse.

indice motore