LA LEGGE DI LENZ

La legge di Lenz prende il nome dal fisico russo Emilij Kristianovic Lenz (1804-1865).

Essa afferma che:

"il verso della corrente indotta in un circuito e' sempre tale da opporsi alla variazione di flusso magnetico che la genera”

Emilij Kristianovic Lenz

Guarda il filmato: Legge di Lenz

SPIEGAZIONE DELLA LEGGE DI LENZ

Visualizzazione del flusso di un campo magnetico B

Per visualizzare il flusso di un campo magnetico B attraverso una superficie S e' utile rappresentare il campo magnetico mediante le sue linee di forza, come indicato in figura:

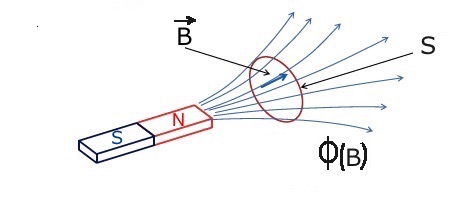
E' stato preso in esame un circuito chiuso, in particolare una spira, alla quale e' concatenato il campo magnatico uniforme generato da una calamita. La definizione di flusso di B attraverso una superficie S e' data dalla relazione:

Φ(B) = B · S = B * S * cosα

dove:

α e' l'angolo compreso tra i vettori B ed S;

S e' il vettore superficie ad essa perpendicolare, il cui modulo e' uguale all'area S della superficie piana presa in considerazione.

Nel caso particolare di figura i vettori B ed S sono paralleli e quindi cosα = cos0⁰ = 1; pertanto, il flusso concatenato con la spira presenta il suo valore massimo:

Φ(B) = B*S

Se il flusso del campo magnetico varia nel tempo, nella spira circolera' una corrente che generera', a sua volta, un campo magnetico (campo indotto). Il campo indotto interagisce con quello iniziale ed il flusso magnetico, dovuto alla corrente indotta nella spira, si opporra' alle variazioni di flusso del campo magnetico iniziale. Pertanto, se il flusso del campo magnetico iniziale cresce, la corrente indotta generera' un campo magnetico che tendera' a compensare l'aumento che l'ha generata.

Come puo' essere prodotta una variazione di flusso di un campo magnetico B?

I casi piu' semplici per produrre una variazione di flusso di un campo magnetico B sono tre:

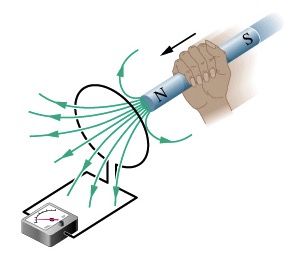
1. Facendo variare il campo magnetico B - per esempio, muovendo un magnete rispetto ad una spira (o viceversa), come mostrato in figura:

   

2. Cambiando la superficie S racchiusa dalla spira - per esempio, deformando la spira, come indicato in figura:

   

3. Facendo ruotare una spira in un campo magnetico uniforme e quindi facendo variare l'orientazione della superficie rispetto alle linee del campo magnetico (cioe' facendo cambiare l'agolo α), come mostrato in figura:

   

Analisi piu' dettagliata del caso relativo allo spostamento di una spira nel campo magnetico generato da una calamita:

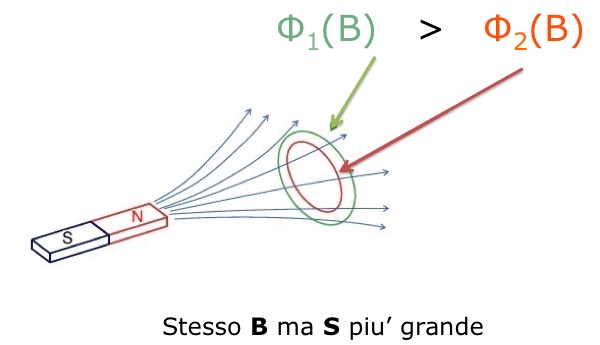
• spira che viene avvicinata al magnete (Fig.1) - in questo caso aumenta il flusso di B attraverso la superficie delimitata dalla spira. Infatti, il flusso e' direttamente proporzionale al numero delle linee di campo che attraversano la spira, percio' quanto piu' la calamita e' vicina alla spira, tanto piu' le linee del campo magnetico uniforme sono numerose e quindi il flusso di B nella spira aumenta.

Nella spira viene indotta una f_em e di conseguenza una corrente:

f_em = - ΔΦ(B)/Δt

I = f_em/R

R = resistenza elettrica del circuito.

Per opporsi all'aumento del flusso, il verso del campo magnetico indotto, deve essere opposto a quello del campo generato dal magnete, cioe' deve essere diretto verso sinistra (Fig.2). Per generare questo campo indotto, la corrente indotta deve scorrere nella spira in senso antiorario se vista dalla parte del magnete:

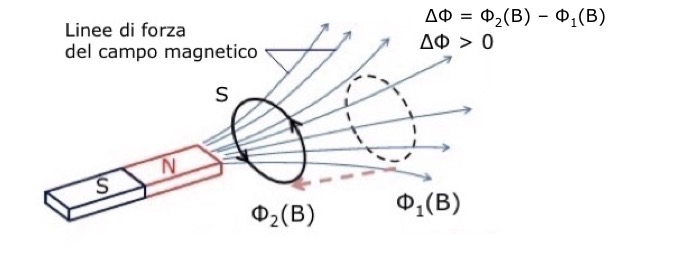Fig.1 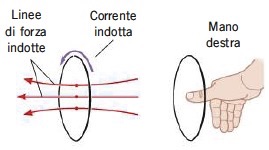Fig.2

Sorgente immagine Fig.2: https://staticmy.zanichelli.it

• spira che viene allontanata dal magnete (Fig.3) - in questo caso il flusso di B nella spira diminuisce ed il campo magnetico indotto si opporra' a questa diminuzione del flusso assumendo lo stesso verso del campo generato dal magnete, cioe' il campo indotto sara' diretto verso destra (Fig.4). Per generare questo campo magnetico indotto, la corrente indotta deve scorrere nella spira in senso orario se vista dalla parte del magnete:

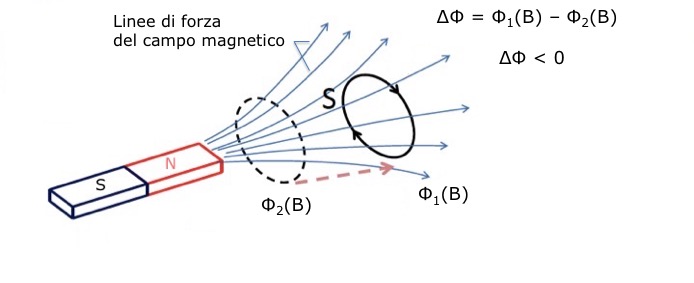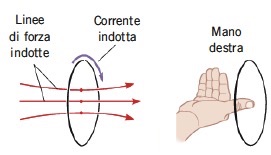Fig.3 Fig.4

Sorgente immagine Fig.4: https://staticmy.zanichelli.it

In definitiva, la corrente indotta in un circuito, prodotta da una variazione del flusso magnetico ΔΦ(B) ad esso concatenato, crea:

• un campo magnetico indotto che e' opposto al campo magnetico esterno se ΔΦ(B) > 0;

• un campo magnetico indotto che ha lo stesso verso del campo magnetico esterno se ΔΦ(B) < 0.

ritorno a "Induzione elettromagnetica”