ritorno a "Struttura e Principio di funzionamento"
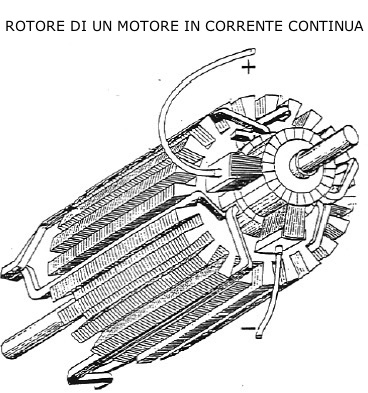
ROTORE DI UN MOTORE ELETTICO IN CORRENTE CONTINUA
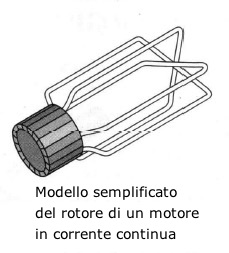
Il rotore del motore rappresenta il cuore del sistema; esso e' costituito da un cilindro in materiale ferromagnetico, nella cui periferia sono ricavate le scanalature (cave) che accolgono gli avvolgimenti. Il rotore e' posizionato all'interno dello statore, il quale produce il campo magnetico. Al rotore e' collegato un collettore a lamelle, sul quale strisciano due spazzole cui e' applicata la tensione di alimentazione.
Ciascun avvolgimento del motore, percorso dalla corrente I, va inteso come una coppia di conduttori diametralmente opposti, ciscuno percorso da corrente in direzione opposta. In altri termini, ai fini del collegamento elettrico, ciascun avvolgimento del motore forma due rami in parallelo e la corrente che scorre in ciascun ramo e' pari ad I/2. L'intensita' della forza F (deducibile dalla Forza di Lorentz) che agisce su ciascun conduttore del rotore e' data dalla relazione:
F = (I/2)*B*L
dove I/2 e' la corrente del singolo conduttore ottenuto dalla ripartizione, effettuata tramite il collettore, dei due rami dell'avvolgimento. Quindi, su conduttori diametralmente opposti si esercitera' una coppia di forze, uguali e contrarie, alle quali e' associato il momento M (momento meccanico), responsabile della rotazione del rotore del motore ed il cui valore e' dato dalla relazione:
M = F*D = B*L*(I /2)*D
dove:
D e' il diametro del rotore in cui sono alloggiati i conduttori;
B e' l'induzione magnetica;
L e' la lunghezza del conduttore.
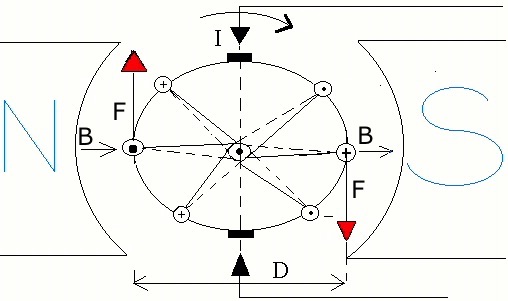
In figura e' riportata una rappresentazione semplificata della sezione del rotore del motore:
La
crocetta, che compare nella figura a destra del rotore, indica una
corrente entrante nel foglio; il puntino, a sinistra del rotore,
indica una corrente uscente dal foglio.
Detto N il numero totale dei conduttori distribuiti sulla periferia del rotore, il momento torcente Tm (coppia motrice), fornito all'asse del motore, e':
Tm = (N/2)*M = (N/2)*(I/2)*B*L*D = [(N*D*L*B)/4]*I
Tm = Kt*I
dove la costante Kt = (N*D*L*B)/4 e' detta costante di coppia del motore e si esprime in (N⋅m)/A.
FORZA CONTROELETTROMOTRICE
Quando il rotore del motore inizia a ruotare, ogni spira (avvolgimento) di cui esso si compone si muove in uno spazio nel quale sono presenti le linee di forza del campo magnetico B uniforme generato dallo statore. La variazione dell'orientazione della superficie di ciscuna spira rispetto alle linee del campo magnetico, causata dal loro movimento, produce una variazione del flusso del campo magnetico concatenato a ciascuna spira. Secondo la legge di Faraday-Neumann-Lenz, se in un certo intervallo di tempo si ha una variazione del flusso del campo magnetico concatenato con un circuito, in esso e' indotta una forza elettromotrice fem (un voltaggio) che genera nello stesso circuito una corrente indotta, il cui verso e' tale da opporsi alla variazione di flusso che l'ha generata.
Nel caso in questione, poiche' la variazione di flusso del campo magnetico, concatenato con gli avvolgimenti del rotore, e' stata provocata dalla tensione di alimentazione che ha permesso il movimento degli avvolgimenti all'interno del campo magnetico di statore, la forza elettromotrice indotta sara' tale da opporsi proprio alla tensione di alimentazione. Si parlera' dunque di forza controelettromotrice, il cui valore e' dato dalla seguente relazione:
fem = [N*Φ(B)]/T
dove N*Φ(B) rappresenta il flusso magnetico tagliato in un periodo T dagli N conduttori in moto.
Si consideri ora una singola spira di filo conduttore immersa in un campo magnetico uniforme B, come illustrato nella figura successiva, nella quale e' stato introdotto il vettore superficie S diretto perpendicolarmente al piano della spira e con intensita' di valore uguale all'area della spira stessa:
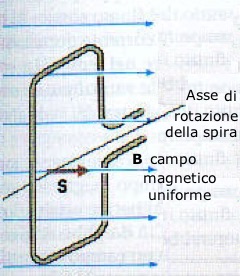
Il flusso del vettore B concatenato con la spira e' definito in generale dalla relazione:
Φ(B) = B · S = B * S * cosα
dove α e' l'angolo compreso tra i vettori B ed S. Nel caso particolare preso in esame e rappresentato dalla figura i due vettori B ed S sono paralleli, per cui: cosα = cos00 = 1. Quindi, il flusso concatenato con la spira presenta il suo valore massimo, dato da:
Φ(B) = S*B
Si faccia ora riferimento alla rotazione degli N avvolgimenti del rotore nel campo magnetico uniforme di statore, ciascun conduttore, in un periodo T, descrivera' una superficie pari alla superficie laterale di un cilindro, il cui valore e':
S = 2π*(D/2)*L = π*D*L
Per la geometria delle espansioni polari, la superficie investita dal flusso del campo magnetico e' pari ad S/2; pertanto, il flusso di B attraverso S/2 e':
Φ (B) = (S/2)*B
ossia:
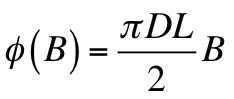
Quindi, l'espressione della forza controelettromotrice diventa:
fem = (N*π*D*L*B)/2T
Sapendo che 1/T = f si puo' scrivere:
fem = f*[(N*π*D*L*B)/2]
Ponendo Ke = (N*π*D*L*B)/2 = Φ(B)*N e ricordando che ω = 2πf, si ha per la forza controelettromotrice:
fem = Ke*f = Ke*(ω/2π)
In definitiva, se si pone K'e = Ke /2π, si ottiene per la forza controelettromotrice la seguente espressione:
fem = K'e*ω
dove K'e = Ke /2π = [Φ(B)*N]/2π = (N*B*L*D)/4 e' la costante di tensione del motore e si esprime in (V⋅s)/rad.
E' importante osservare che, pur essendo Kt = K'e, queste due costanti hanno una diversa denominazione per il fatto che si misurano in unita' diverse. L'uguaglianza delle costanti Kt e K'e permette di introdurre la costante di macchina del motore: Cm = Kt = K'e.